A Brief Discussion of Fractals

One of the most essential concepts to understand these graphs is the concept of recursion. Like the matryoshka dolls, the simple concept is that one performs an action on the same set of objects that one just performed. With the dolls, one opens a doll, takes out the doll inside, then takes that doll and opens it, then takes that doll...this is the concept of recursion. This concept is used many times in life. Filing documents, we look at the data key and check that against the file cabinets, then against the drawers, then against the files in the drawer, then often we look at another piece of information to sort within the file. Same data (the file), same process (what is the key versus the groupings), repeated until we have our desired result.

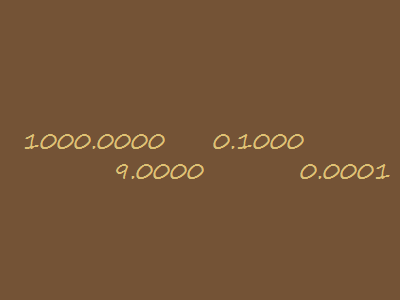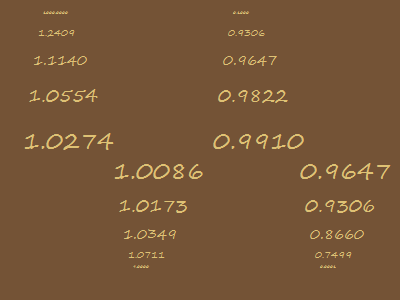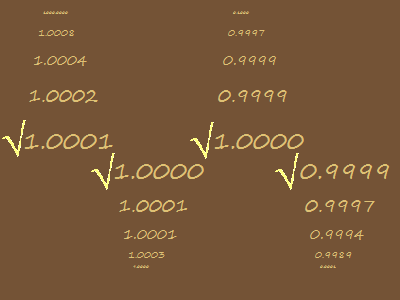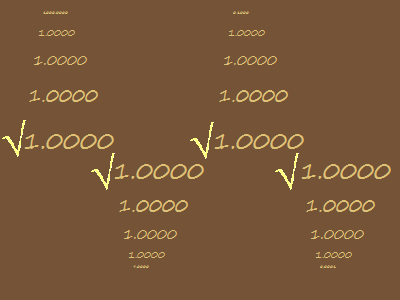This can be done with math functions as well. Clicking on the box to the right will open an animation showing the square root function run over four different starting numbers, recursively. That is, the square root of 1,000 is found, then the square root of that result is found, and so on. Starting at numbers greater than one or less than one, we see that the square root function will always end up at 1. This process is called computing an orbit of a function and a point such as 1 for the square root function is called an attractor.

The concept of attractors in detail is beyond the scope of this website. The result, though, that repeating the square root over a real number and it moves inexorably towards 1 is called convergence. Like many people moving towards a gate at once, converging on a point of entry, so too is the function converging on a point. Opposite of this is divergence, everything moving apart. This will be discussed in greater detail on the Mandelbrot Set page.

Repetition is also used to create shapes such as the Sierpinski Sieve, shown left (again, clickable for animation). Starting with a single triangle or square, a triangle is cut out of the middle. This leaves one large triangle composed of three smaller triangles. The process is then recursed on each smaller triangle, and so on with the nine resulting triangles, etc. etc. to infinity. In the end we have a two dimensional shape that has a total surface area of zero, and a very cool picture.

Other shapes created with this process of repetition are the Cantor Set, the Koch Curve, the Mandelbrot Set and Iterated Function Systems. Hence, it is important to understand the concept of repeating an action over a small set of data before moving on.