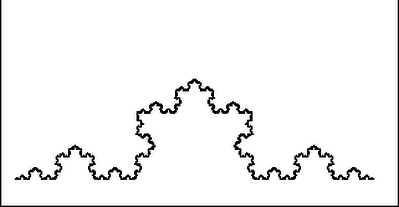
Helge von Koch described the next shape we'll be investigating, in 1904. The process of creating a Koch Curve is quite similar to a Cantor Set.

Typically, one takes a line segment, again we'll call it of length 1, and again we cut out the middle third. However, instead of leaving this space empty, we'll make a 'hat' for it with line segments of equal length to the remaining segments from the cut. This will also create angles of sixty degrees, the same as an equilateral triangle. Now we have a curve that is 4/3s long, and we can take each of these line segments and repeat the process. Here is an animation that shows the transformation from a single line segment to a Koch Curve:

An animated Koch Curve


Traditional Koch motif Another method of construction is to apply a motif to a line segment. That is, we take an initial motif such as the one on the right and we apply it again and again to each line segment we find. This process is more general because it can be done with a variety of motifs on a variety of initial shapes. What we draw here is known as the Koch Curve, but following the link at the bottom of the page to more information, we can see such things as Koch Snowflakes and more.

Again, we now wonder what is the resultant length, if the process is allowed to go to infinity, and what is the dimension of a Koch Curve. First, the length, again the first few results:

The results are getting large, and they continue to grow and grow. After a mere 128 repetitions, the length of all the line segments together is greater that one light year. Still, though, the curve has a width of 1 and height of 1.15470. What we have is an object that is of infinite length in a finite space.

With computations that are beyond the scope of this page, the dimension of the curve is shown to be 1.26186. That is, it's more than a line but less than a surface.

Here is more information, at a much higher level of discussion, at Wikipedia.